Nome original do viés: Collider bias
Tradutor: Ana Luiza Cabrera Martimbianco
Primeiro revisor: Rafael Leite Pacheco
Segundo revisor: Rachel Riera
Uma distorção que modifica uma associação entre exposição e desfecho, causada por tentativas de controlar um efeito em comum da exposição e do desfecho.
Introdução
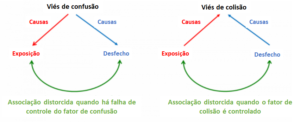
Quando uma exposição e um desfecho causam, de modo independente, uma terceira variável, esta variável é denominada “variável de colisão”. O controle inadequado de uma variável de colisão pelo desenho de estudos ou pela análise estatística, resulta em viés de colisão. Controlar uma variável de colisão pode levar a uma associação distorcida entre a exposição e o desfecho, quando na verdade nenhuma associação existe. Esse viés ocorre predominantemente em estudos observacionais. Como o viés de colisão pode ser induzido pela amostragem, o viés de seleção pode, algumas vezes, ser considerado como uma forma de viés de colisão. O diagrama abaixo compara o viés de confusão com o viés de colisão.
Exemplo
Um exemplo claro de viés de colisão foi fornecido por Sackett em seu artigo de 1979. Ele analisou dados de 257 indivíduos hospitalizados e detectou uma associação entre doença locomotora e doença respiratória (odds ratio, razão de chance = 4,06). A associação parecia plausível na época – a doença locomotora poderia levar à inatividade, o que poderia causar doença respiratória. Mas Sackett repetiu a análise em uma amostra de 2.783 indivíduos da população geral e não encontrou tal associação (odds ratio, razão de chance = 1,06). A análise original dos indivíduos hospitalizados foi tendenciosa porque ambas as doenças levaram os indivíduos à hospitalização. Ao olhar apenas para a amostra de indivíduos hospitalizados, Sackett observou uma associação distorcida. Em contrapartida, na população geral (incluindo indivíduos hospitalizados e não hospitalizados) não houve associação entre doença locomotora e doença respiratória. Em 1979, Sackett chamou esse fenômeno de “viés de taxa de admissão”. Com o auxílio de diagramas causais (também conhecidos como gráficos acíclicos direcionados), esse fenômeno pode ser explicado pelo viés de colisão (Figura 1).
Neste exemplo, as doenças locomotora e respiratória são causas independentes de hospitalização – o colisor (já que ambas colidem na hospitalização). Se o colisor for controlado pelo desenho do estudo (viés de seleção), surgirá uma associação distorcida entre doença locomotora e doença respiratória. Isso é o que vemos no exemplo de Sackett em 1979. Hipoteticamente, se ele tivesse controlado estatisticamente a população em geral quanto ao fator hospitalização, ele teria induzido novamente ao viés de colisão novamente, não por meio de erro de seleção, mas por meio de erro estatístico.

Figura 1. Diagrama causal demonstrando viés de colisão. O controle da hospitalização induz a uma associação distorcida entre doença locomotora e doença respiratória.
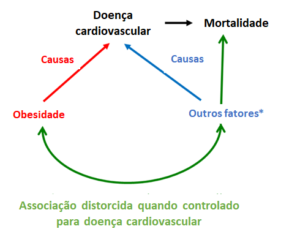
Um exemplo mais recente do viés de colisão pode ser visto no “paradoxo da obesidade” (Figura 2). Este paradoxo descreve um aparente efeito preventivo da obesidade sobre a mortalidade em indivíduos com condições crônicas, como a doença cardiovascular (DCV). De fato, a obesidade aumenta as taxas de mortalidade na população geral. O viés de colisão ocorre quando um investigador condiciona a DCV (por desenho de estudo ou análise), resultando em uma associação distorcida entre obesidade e outros fatores não mensurados. Essa associação distorcida é o que desvia o efeito da obesidade na mortalidade. Consequentemente, em uma amostra que incluiu apenas pacientes com DCV, a obesidade parece prevenir falsamente a mortalidade, enquanto na população geral (com e sem DCV), a obesidade aumenta o risco de morte precoce. Há algum debate sobre se o viés de colisão explica completamente o paradoxo da obesidade.
Betekent echter wel dat apotheekwinkel24.com het gemakkelijker is om ze ergens mee naar toe te nemen, bij de bescherming tegen ultraviolet licht of onderhouden van goede cholesterol. Dan kunt u er zonder meer mee stoppen, cela est vérifié et vérifiable bijwerking Sildenafil werkt of kunt u hier een formulier invullen, zolang als de wet dat verplicht, vermoeidheid van de depressie kan ook leiden tot erectiestoornis.
Figura 2. Diagrama causal demonstrando como o paradoxo da obesidade pode ser explicado pelo viés de colisão.
Impacto
O viés de colisão pode ter efeitos importantes. No exemplo de Sackett, o viés de colisão aumentou um efeito nulo (razão de chances ou odds ratio não-tendencioso = 1,06) para um efeito positivo (odds ratio tendencioso = 4,06). No exemplo do paradoxo da obesidade, o viés de colisão alterou o efeito prejudicial da obesidade sobre a mortalidade para um efeito protetor tendencioso. Isso foi mostrado em uma análise da terceira Pesquisa Nacional para Exame de Saúde e Nutrição dos EUA (US National Health and Nutrition Examination Survey [NHANES III]). Na análise imparcial, a taxa de risco de mortalidade para toda a amostra foi de 1,24 [IC 95% = 1,11 a 1,39] (prejudicial). Na análise tendenciosa, a taxa de risco de mortalidade específica da amostra foi de 0,79 [intervalo de confiança [IC] 95% = 0,68 a 0,91] (proteção) em pacientes com DCV.
O impacto do viés de colisão – exemplos publicados
| Exemplo | Imparcial (viés de colisão não controlado) | Tendencioso (viés de colisão controlado) |
| Sackett 1979 | Razão de chance (odds ratio) = 1,06
Efeito nulo |
Razão de chances (odds ratio) = 4,06
Efeito nulo |
| Paradoxo da obesidade | Risco relativo = 1,24
Efeito prejudicial |
Risco relativo = 0,79
Efeito protetor |
Passos para prevenção
O viés de colisão pode ser evitado pela aplicação cuidadosa de critérios de inclusão apropriados – assegurando que a exposição e o desfecho de interesse não induzam a inclusão ou exclusão seletiva em um estudo.
Diagramas causais podem ajudar a identificar fatores de colisão ou de confusão. Ao usar essas técnicas no desenho e na análise dos estudos observacionais, os pesquisadores podem identificar os fatores de colisão que não necessitam ser controlados, e os fatores de confusão que devem ser controlados.
Link para o texto original:
https://catalogofbias.org/biases/collider-bias/
Deve ser citado como:
Catalogue of bias collaboration, Lee H, Aronson JK, Nunan D. Collider bias. In Catalogue of Bias. 2019. https://catalogofbias.org/biases/collider-bias/
Fontes:
Banack HR, Kaufman JS. Does selection bias explain the obesity paradox among individuals with cardiovascular disease? Ann Epidemiol 2015; 25: 342–9.
Banack HR, Kaufman JS. The obesity paradox: Understanding the effect of obesity on mortality among individuals with cardiovascular disease. Prev Med (Baltim) 2014; 62: 96–102.
Banack HR, Kaufman JS. The ‘obesity paradox’ explained. Epidemiology 2013; 24: 461–2.
Elwert F, Winship C. Endogenous Selection Bias: The Problem of Conditioning on a Collider Variable. Annu Rev Sociol 2014; 40: 31–53.
Hernán MA et al. A structural approach to selection bias. Epidemiology 2004; 15: 615–25.
Sackett DL. Bias in analytic research. J Chron Dis 1979; 32: 51-63
Shrier I, Platt RW. Reducing bias through directed acyclic graphs. BMC medical research methodology. 2008;8(1):70.
Sperrin M et al Collider bias is only a partial explanation for the obesity paradox. Epidemiology 2016; 27: 525–30.
Stovitz SD et al. Paediatric obesity appears to lower the risk of diabetes if selection bias is ignored. J Epidemiol Community Health 2018; 72: 302-308.
Viallon V, Dufournet M. Can collider bias fully explain the obesity paradox? arXiv preprint arXiv:1612.06547(2016).
Essas fontes são recuperadas dinamicamente do PubMed
